
第 7 回のテーマは「 奇数と偶数 , 三角数と四角数 」です。
なんとなく分かった気でいた「 奇数と偶数 」を、しっかり定義として理解しておこうと思います。
「 三角数と四角数 」というものは、恥ずかしながら自分は知らなかったのですが、これは「 数列の和 」の話です。
数列というと自分は、高校で習うような難しいイメージを持つのですが、三角数と四角数の仕組みはシンプルで、数列に慣れるにも良いと思います。
三角数は「 1 から特定の自然数までの和 」を表し、四角数は「 1 から数えて \(n\) 番目までの奇数の和 」を表します。
それでは、これらを順番に見ていきたいと思います。
奇数と偶数
整数は、2 で割り切れる「 偶数 」と、2 で割った時に 1 余る「 奇数 」に分けられます。
ちなみに「 0 」は 2 で割っても余りが出ないので「 偶数 」です。
また奇数と偶数は交互に現れるので( 偶数に +1 or -1 すると奇数、奇数に +1 or -1 すると偶数 )、1 ( 奇数 )から 1 引いた「 0 は偶数 」です。
「 偶数 」\(\pm\)「 偶数 」=「 偶数 」であり、「 奇数 」\(\pm\)「 奇数 」=「 偶数 」
このように「 同じもの同士は 」足しても引いても「 偶数 」です。
「 偶数 」\(\pm\)「 奇数 」or「 奇数 」\(-\)「 偶数 」=「 奇数 」
このように「 違うもの同士は 」足しても引いても「 奇数 」になります。
また、掛け算の場合では、
「 偶数 」×「 偶数 」=「 偶数 」であり、「 奇数 」×「 偶数 」=「 偶数 」です。
これは、偶数+偶数=偶数なので、いくつ足そうが偶数。1 余るものでも「 偶数個 」あれば「 奇数+奇数=偶数 」のペアができるので「 割り切れる 」からです。
「 奇数 」×「 奇数 」=「 奇数 」このように「 奇数同士を掛けた時 」だけ「 奇数 」になります。
これは、奇数のペアを作っても、「 1 つ奇数が残る 」ので奇数です。
まとめ
以上を整理してまとめると、「 \(n\) 」が整数のとき、( \(n\) は number の \(n\) つまり数のことです )
偶数とは「 \(2n\) ( 2 の倍数が偶数 ) 」であり、奇数とは「 \(2n-1\) ( 偶数から 1 引くと奇数 ) 」となります。
ちなみに、奇数は \(2n+1\) と表すこともありますが、どちらにしても偶数に「 1 を足す 」or 偶数から「 1 を引く 」と奇数ということです。
使い分けとしては「 \(n\) 」 に「 自然数 」を入れて「 正の奇数 」を求めるときには「 \(2n-1\) 」を使い、
「 \(n\) 」に「 負の整数 」を入れて「 負の奇数 」を求めるときには「 \(2n+1\) 」を使うと使いやすいです。
これにより、例えば「 3 番目( 3 つ目 , 3 個目 )の奇数は何か? 」を求める場合、
「 \(2n-1\) 」の \(n\) に 3 を代入して、2 × 3 − 1 = 5 となり、3 番目の奇数は 5 と出せます。( 1 , 3 , 5 で 3 番目 )
三角数とは
三角数とは「 ● を正三角形に並べた時の、● の個数( 合計数 ) 」のことです。
これは「 1 から特定の自然数までの和 」にもなっています。

上図のように、
- 1 番目の三角数( 1 までの自然数の和 )は、1
- 2 番目の三角数( 2 までの自然数の和 )は、1+2 で 3
- 3 番目の三角数( 3 までの自然数の和 )は、1+2+3 で 6
- 4 番目の三角数( 4 までの自然数の和 )は、1+2+3+4 で 10
三角数は「 自然数を積み上げた数 」になっています。これは 1 つ前の結果から、次の結果が求められるという仕組みです。
例えば、3 番目の三角数が 6 なら、4 番目の三角数は「 3 番目の三角数に、一番下の 4 つを付けたもの 」になっています。
つまり「 6 ( 1 つ前の結果 ) + 4 ( 求める順番 ) = 10 」という仕組みです。
同様に、5 番目の三角数を求めるなら「 10 ( 4 番目の三角数 )+ 5 ( 求める順番、一番下の増えた分 )= 15 」となります。
そしてこれは「 1 から 5 までの数の足し算の結果 」でもあります。( 1+2+3+4+5=15 )
三角数( 自然数の和 )の公式
では、1 つ前の三角数が分からない時は、どうしたら良いのでしょうか。
考え方として、三角数の形を上下逆にしても、もちろん数は変わりません。なのでもう 1 つ逆向きの三角数を並べ、両者をくっつけて見ます。
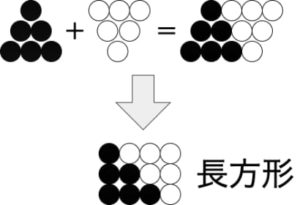
すると上図のように、結果的に「 長方形 」になり、簡単に計算できます。最後に 2 で割れば( 2 つの三角数を合わせたものなので )、三角数の値が求められます。
図の例「 3 番目の三角数 6 」で証明すると、縦が 3 (つ) 横が 4 (つ)の長方形になるので、3 × 4 = 12 と合計数が求まり、これを 2 で割り 12 ÷ 2 = 6 と求められます。
また、100 番目の三角数だと、縦が 100 横が 100+1 の長方形が作れるので、100 ×( 100+1 ) ÷ 2 = 5050 となり「 1 から 100 までの和 」は 5050 と出せます。
以上の証明から、三角数( 自然数の和 )の公式「 \(n\) 番目の三角数 」は \(n\left(n+1\right)\div2\) となります。
つまり、\(\displaystyle\frac{n\left(n+1\right)}{2}\) という形になります。
四角数とは
四角数とは「 ○ を正方形に並べた時の、○ の個数( 合計数 ) 」のことです。
これは「 1 から数えて \(n\) 番目までの奇数の和 」にもなっています。
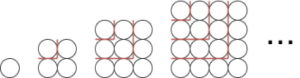
上図のように、
- 1 番目の四角数( 1 番目 , 1 つ目までの奇数の和 )は 1
- 2 番目の四角数( 2 番目 , 2 つ目までの奇数の和 )は 1+3 で 4
- 3 番目の四角数( 3 番目 , 3 つ目までの奇数の和 )は 1+3+5 で 9
- 4 番目の四角数( 4 番目 , 4 つ目までの奇数の和 )は 1+3+5+7 で 16
図の赤い線で区切っている所が、奇数になっており、四角数は「 奇数の和 」で構成されています。
四角数( 奇数の和 )の公式
四角数は「 正方形 」なので「 縦と横の数が同じ 」です。よって同じ数( 縦の数と横の数 )を掛ければ、つまり「 2 乗 」すれば ○の個数( 合計数 )が出せます。
- 2 番目の四角数は 2 × 2 = \(2^2\) = 4
- 3 番目の四角数は 3 × 3 = \(3^2\) = 9
- 4 番目の四角数は 4 × 4 = \(4^2\) = 16
- 100 番目の四角数は 100 × 100 = \(100^2\) = 10000
以上から、四角数( 奇数の和 )の公式「 \(n\) 番目の四角数 」は \(n\times n\) つまり「 \(n^2\) 」となります。
このように、四角数とは 2 乗数なので「 平方数 」と呼ばれます。これは「 正方形の面積 」そのものでもあります。
四角数( 奇数の和 )の例題
例えば「 49 までの奇数の和を求める 」場合
まず、「 49 」という奇数が「 何番目の奇数 」なのかを調べます。
ここで先ほどの「 奇数の求め方 」を使います。49 は自然数の奇数( 正の奇数 )なので「 \(2n-1\) 」を使うと、
\(2n-1=49\) であり、これを解くと \(n=25\) つまり「 25 番目の奇数が 49 」ということが分かりました。
ここから、25 番目の四角数( 25 個の奇数の和 )つまり 49 までの奇数の和を求めます。
四角数の公式「 \(n^2\) 」の \(n\) に 25 を代入すると、\(25^2=625\) となります。
よって「 49 までの奇数の和は 625 」ということです。
まとめ
このように、\(n\) 番目の四角数( \(n\) 番目までの奇数の和、\(n\) 個の奇数の和 )の求め方「 \(n^2\) 」と、
\(n\) 番目の正の奇数の求め方「 \(2n-1\) 」負の奇数の求め方「 \(2n+1\) 」を使えば、
どんな数でも、その特定の数までの「 奇数の和 」を出すことができます。
あとがき
今回は「 奇数と偶数 」から「 三角数と四角数 」という話でした。
自分は三角数と四角数だけでなく、奇数や偶数も定義としては全く解っておらず、今回初めて整理して理解できました。
そして三角数( 自然数の和 )と四角数( 奇数の和 )というのは、面白い仕組みで出来ているんだなと感じました。数学って、解っていくと楽しいものなのかも知れません。
最後までお読み頂きまして、誠にありがとうございました。



